Math on Demand

AG Analysis, Prof. Haller

Eine Linie ist 1-dimensional, ein Quadrat 2-dimensional und eine Kugel hat Dimension 3. Der Begriff der Dimension ist so intuitiv und klar, dass man selten darüber nachdenkt. Die Kochsche Schneeflocke ist ein einfaches Beispiel eines Fraktals und zeigt eindrucksvoll, dass der Dimensionsbegriff komplizierter und interessanter ist als man denken möchte. Wir werden sehen, dass die Kochsche Schneeflocke eine Linie ist, die nicht Dimension 1 hat.

Der Vortrag stellt die Kochsche Schneeflocke vor und thematisiert die Frage, wie man den intuitiven Begriff der Dimension mathematisch exakt beschreiben kann. Er stellt die Grundidee der Hausdorff-Dimension vor und am Ende wird die Dimension der Kochschen Schneeflocke exakt bestimmt.

Zielgruppe: Oberstufe

Vorkenntnisse: Termumformungen, Flächeninhalt Dreieck

Zeitrahmen: 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Logik, Prof. Otto

Die Aussagenlogik oder boolesche Logik (nach George Boole, 1815 – 1864) erlaubt es, Information über Situationen, die anhand von Ja/Nein-Fragen (d.h. bit-weise) beschrieben sind, mit mathematischen Methoden logisch und algebraisch zu bearbeiten. Schon auf diesem Niveau gibt es interessante Methoden und überraschende Gesetzmäßigkeiten zu entdecken.

Beim Folgerungsproblem zum Bespiel geht es um die Frage, ob eine Reihe von Bedingungen eine bestimmte logische Konsequenz allgemein nach sich zieht. Vgl. das Faksimile einer Denksportaufgabe von Charles Dodgson, alias Lewis Carroll, 1832-1898).

Wenn mehrere potentielle Beschreibungen und unterschiedliche Verfügbarkeit von Information eine Rolle spielen, wird die Modellierung von wechselseitigen Abhängigkeiten eine spannende Aufgabe, die im Rahmen der sogenannten Modallogik behandelt werden kann. Hier geht es u.a. um das Argumentieren mit Aussagen über das Wissen verschiedener Personen, wie es oft in strategischen Szenarien vorkommt: „Wenn A weiß, dass B nicht weiß, welche Karte A gezogen hat, dann…“

In Kurzvorlesungen und Gruppenübungen stehen die mathematische Modellierung, die logische Systematik und die Exploration anhand von Beispielaufgaben im Vordergrund.

Zielgruppe: Oberstufe

Vorkenntnisse: Bekanntschaft mit elementaren Konzepten wie Mengen, Relationen, Funktionen, Aussagen ist hilfreich.

Zeitrahmen: mehrere Sitzungen

Format: Schüler-Workshop mit Kurzvorlesungen und Gruppenübungen

AG Didaktik, Prof. Kümmerer

Warum beschäftigen sich Mathematikerinnen und Mathematiker mit Knoten? Neue Knoten für Seeleute oder für neue Strickmuster?

Der Weg der Knoten in die Mathematik ist verschlungener. Navigationsprobleme der weltreisenden Seefahrer brachten den großen Mathematiker Carl Friedrich Gauß zu den Knoten. Ein paar Jahrzehnte später sollten Knoten das System der chemischen Elemente ordnen. Und wir alle verdanken unser Leben der Tatsache, dass seit vielen Millionen Jahren jede Zelle bei ihrer Teilung ein Entknotungsproblem löst, dem die Mathematik erst in den letzten dreißig Jahren auf die Spur kommt -- und dies als einen ihrer größten Fortschritte im 20. Jahrhundert ansieht.

Wir verfolgen den Weg der Knoten durch die Mathematik und erleben, dass Mathematik mehr ist als Rechnen und Jonglieren mit Zahlen, dass mathematische Lösungen eines Problems oft ganz unerwartet neue Anwendungen finden und nicht zuletzt, dass man auch mit Schulkenntnissen an modernen Entwicklungen der Mathematik teilhaben und vielleicht sich sogar für sie begeistern kann.

Zielgruppe: Oberstufe

Vorausgesetzte Vorkenntnisse: Rationale Funktionen

Zeitrahmen: 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Logik, Prof. Otto

Die Idee unendlich großer und unendlich kleiner Größen fasziniert seit Jahrtausenden, nicht nur in mathematischer Hinsicht. Eine mathematisch fundierte Theorie unendlicher Größen wurde von Georg Cantor (1845--1918; besuchte in Darmstadt die Schule) gegeben; die von ihm begründete axiomatische Mengenlehre analysiert unterschiedliche Grade von Unendlichkeit im Größenvergleich von Mengen. Auch kombinatorische Fragen im Unendlichen bieten eine interssante Herausforderung für das Vorstellung- und Abstraktionsvermögen, wie zum Beispiel in diesem Gedankenexperiment:

Teilnehmer 1,2,3,… an einem Quiz bekommen je eine eigene ja/nein-Frage; sie kennen vorab nicht die Fragen, aber sie wissen, dass jeder die richtige Antwort auf die Fragen aller anderen kennen wird, nicht aber auf die eigene. Könnten sich die Teilnehmer vorab so absprechen, dass insgesamt nur endlich viele falsche Antworten gegeben werden?

Mit unendlich kleinen Größen – „Infinitesimalien“ – arbeiteten Isaac Newton (1642--1727) und Gottfried Wilhelm Leibniz (1646--1716) in ihrer Entwicklung der Analysis. Die Verwendung von Infinitesimalien wurde erst durch Abraham Robinson (1918--1974) in der sogenannten Nichtstandardanalysis mit logischen Methoden voll gerechtfertigt. Hier werfen wir einen abstrakten Blick ins unendlich Kleine – eine Perspektive, die die üblichen Grenzprozesse der Differential- und Integralrechnung überraschend einfach aussehen lassen kann.

Zielgruppe: Oberstufe

Vorkenntnisse: Bekanntschaft mit elementaren Begriffen wie Mengen, Funktionen und einfachen Konzepten der Algebra und Analysis

Zeitrahmen/Format: Schülerworkshop (mehrere Sitzungen) oder Vortrag (90min)

AG Didaktik, Prof. Kümmerer

Nachdenken über das Unendliche – das Undenkbare Denken – ist ein großes Abenteuer. Schon im Alltag begegnet uns das Unendliche: Es gibt unendlich viele Zahlen, zwischen zwei Spiegeln können wir uns unendlich oft sehen und parallele Schienen scheinen sich im Unendlichen zu schneiden. Ausgehend von diesen Erfahrungen verfolgen wir die Auseinandersetzung mit dem Unendlichen aus kulturgeschichtlicher und mathematischer Sicht.

Unglaubliches hält das Unendliche für uns bereit: Ein Teil kann so groß sein wie das Ganze, und dennoch ist es mit einer Unendlichkeit nicht getan. Unheimlich war das Unendliche schon den Griechen. Wie sie damit umgingen, beeinflusst seither die Mathematik. Unmöglich scheint das Unendliche, das zeigten schon die Paradoxien des griechischen Philosophen Zenon. Sie sind bis heute eine spannende Herausforderung für die Mathematik, der Wissenschaft vom Unendlichen.

Zielgruppe: Oberstufe

Vorausgesetzte Vorkenntnisse: Schulstoff bis etwa Klasse 11. Klasse

Zeitrahmen: 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Geometrie, Prof. Reif

Subdivisionsalgorithmen sind mathematische Verfahren, mit deren Hilfe sich glatte Kurven und Flächen im Computer auf einfache Weise berechnen und darstellen lassen. Sie werden heute vor allem bei der Herstellung computer-animierter Filme eingesetzt, ihre mathematische Untersuchung stellt aber bis heute eine Herausforderung dar. In diesem Vortrag wird die Geschichte dieser faszinierenden Algorithmen erzählt. Sie beginnt mit einem Hammer in Lausanne und endet mit einem Oscar in Hollywood.

Zielgruppe: Oberstufe

Vorausgesetzte Vorkenntnisse: keine speziellen Vorkenntnisse

Zeitrahmen: 45 – 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Numerik, Dr. Gerisch

Beim Auspacken der Zutaten für mehrere Sorten Plätzchen ging ein Ei zu Bruch. Wieviel kann jetzt von welchem Rezept gebacken werden, damit keine Zutaten übrig bleiben? Dieses Problem können wir als lineares Gleichungssystem schreiben, dessen Lösung uns die Antwort liefert.

Im alltäglichen Leben begegnen uns oft lineare Gleichungssysteme. Kleine Systeme (mit zwei oder drei Unbekannten) lassen sich gut von Hand lösen. Mit zunehmender Anzahl der Unbekannten/Gleichungen wird die Lösung per Hand allerdings sehr aufwändig.

Wir lernen das Gauß-Verfahren und seine algorithmische Umsetzung kennen, gehen auf Schwierigkeiten und Herausforderungen ein und lernen alternative Methoden zur näherungsweisen Lösung von linearen Gleichungssystemen kennen.

Zielgruppe: Oberstufe

Vorausgesetzte Vorkenntnisse: lineare Gleichungssysteme

Zeitrahmen: 45 – 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Stochastik, Prof. Aurzada

Sir Francis Galton beschäftigte im Jahr 1873 die Frage, mit welcher Wahrscheinlichkeit ein Familienname ausstirbt. Diese Frage wurde anschließend von Reverend Henry William Watson untersucht. Nach diesen beiden Wissenschaftlern ist das erste Modell für Populationsentwicklungen benannt, das den Zufall miteinbezieht, der Galton-Watson-Verzweigungsprozess. Dieses Modell wird auch zur Modellierung der Ausbreitung von Krankheiten oder Viren (wie dem Coronavirus) benutzt. Im Vortrag wird das mathematische Modell vorgestellt und in den verschiedenen Kontexten interpretiert.

Zielgruppe: Oberstufe

Vorausgesetzte Vorkenntnisse: Funktionen, insbesondere Polynome; Ableitung von Funktionen; Verkettung von Funktionen; idealerweise: Grundkenntnisse in Stochastik

Zeitrahmen: 45 – 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Algebra, Prof. Kümmerer

Mathematik war mehr als zweitausend Jahre die unbestrittene Königin der Wissenschaften. Und heute? „Keiner liebt mich“ hört man sie sagen. Der Schulunterricht scheint oft folgenlos zu bleiben, Mathematik zeigt sich im Alltag kaum. Eine Bestandsaufnahme ihrer Rolle im allgemeinen Bewusstsein leitet den Vortrag ein.

Mathematik weckt Gefühle wie kaum eine zweite Wissenschaft: Von Angst über Bewunderung bis zu Begeisterung, und auch die Werbung spielt mit diesen Gefühlen. Sie stehen im Mittelpunkt des zweiten Teils des Vortrages.

Mathematik durchdringt unseren Alltag, mehr als je zuvor, man muss nur hinschauen. Einige Beispiele machen das deutlich. Unsere Zukunft wird auch davon abhängen, dass sich breite Teile der Gesellschaft wieder mit der Mathematik aussöhnen. Wege zur Versöhnung beschließen den Vortrag.

Zielgruppe: Mittelstufe/Oberstufe

Vorausgesetzte Vorkenntnisse: Keine

Zeitrahmen: 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Numerik, Prof. Giesselmann

Mathematik ist eine exakte Wissenschaft. Um physikalische Modelle mit mathematischen Methoden exakt zu lösen,

müssen oft unrealistische Vereinfachungen angenommen werden. Die Mathematik bietet aber Werkzeuge, mit denen wir

auch realistische Modelle lösen können – Werkzeuge, die Lösungen approximieren und auf den ersten Blick scheinbar

ungenau sind.

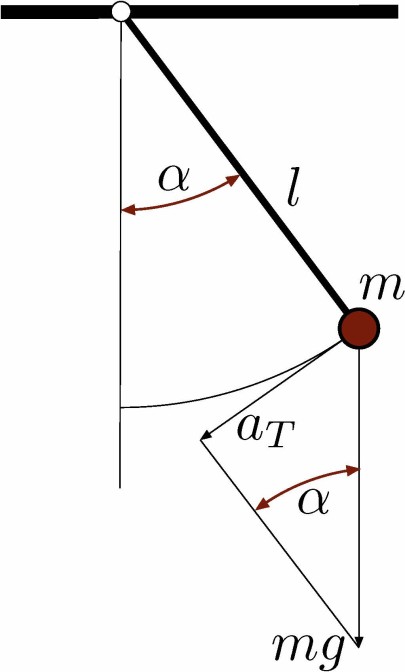
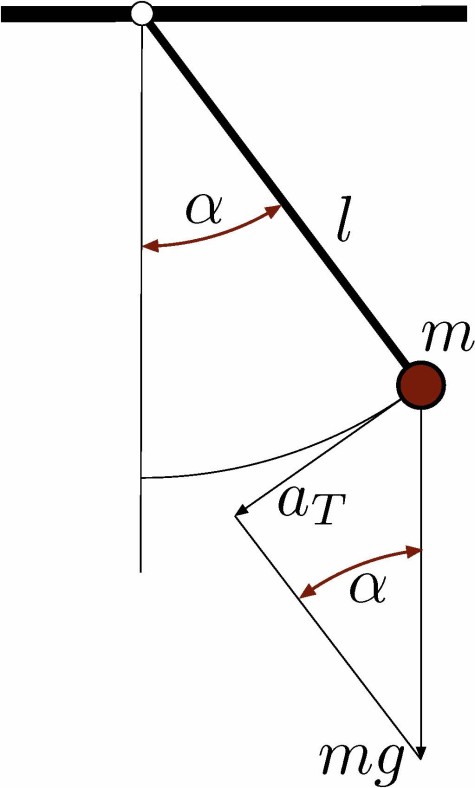
Der Vortrag taucht ein in die Welt des Modellierens von physikalischen Vorgängen und deren Lösung. Anhand eines

einfachen Pendelmodells erklären wir die Bedeutung von numerischen Methoden, die mit Hilfe der Mathematik genau

analysiert werden können. Elegante Mathematik und das Lösen von praktischen Problemen widersprechen sich eben

nicht! Es ist vielmehr ein Zusammenspiel der sogenannten MINT Fächer gefragt!

Zielgruppe: Oberstufe

Vorausgesetzte Vorkenntnisse: physikalische Grundkenntnisse (Pendel), Ableitung, Tangente

Zeitrahmen: 45 – 60 min

AG Analysis, Prof. Haller

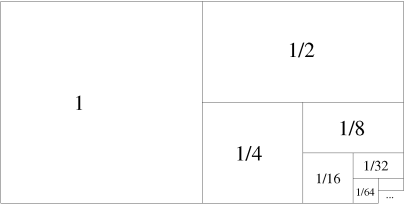
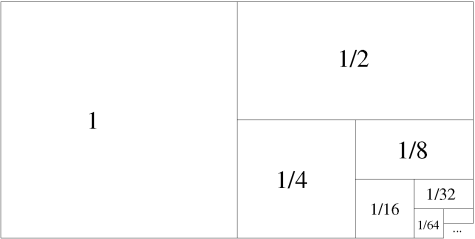
Der exakte Umgang mit dem unendlich Großen und unendlich Kleinen ist ein wichtiges Thema in der Mathematik und ein Grund für ihre erfolgreiche Verwendung als Sprache der Naturwissenschaften.

Anhand der unendlichen Summation von Zahlen wird in diesem Vortrag gezeigt, dass das Unendliche sich nicht immer intuitiv verhält und man beim Umgang damit altbekannte Gewissheiten in Frage stellen muss.

Zielgruppe: Mittelstufe, Oberstufe

Vorausgesetzte Vorkenntnisse: Bruchrechnung

Zeitrahmen: 30min bis 60min

Format (max. Teilnehmerzahl): Vortrag (beliebig)

AG Logik, Prof. Otto

Situationen mit selbstbezüglicher Zirkuläritat haftet oft etwas Paradoxes an, und man tut sie als „unmöglich“ ab. Ein bekanntes klassisches Beispiel wird Epimenides (7.Jh.v.Chr.) zugeschrieben. Der Kern seines Lügner-Paradoxons lässt sich auf den Status der Aussage „diese Aussage ist nicht wahr“ reduzieren. Selbstbezüglichkeit und eine Negation wirken hier ähnlich paradox zusammen wie die verdrillte Verklebung der Winkelschenkel in der hier abgebildeten (scheinbaren) Perspektivskizze.

In der Mathematik kann man mit Ideen, die eine ähnliche Selbstbezüglichkeit haben, oft interessante Einsichten erzielen — insbesondere Objekte finden, die einen gegebenen Bezugsrahmen sprengen und darüber hinausweisen. Man spricht in diesem Zusammenhang von Diagonalisierungsargumenten. Der Vortrag begleitet auf einem Streifzug von Epimenides über Cantor und Russell (Mengenlehre), Turing (Berechenbarkeit) und Gödel (mathematische Logik).

Zielgruppe: fortgeschrittene Mittelstufe/Oberstufe

Vorkenntnisse: Bekanntschaft mit elementaren Konzepten wie Mengen, Aussagen, Berechnungsverfahren ist hilfreich, aber nicht notwendig

Zeitrahmen: 60min, 90min

Format (max. Teilnehmerzahl): Vortrag (beliebig)