Darmstadt Graduate School of Excellence Energy Science and Engineering
Optimal control of scalar transport in incompressible fluid flow
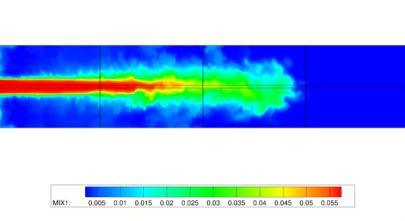
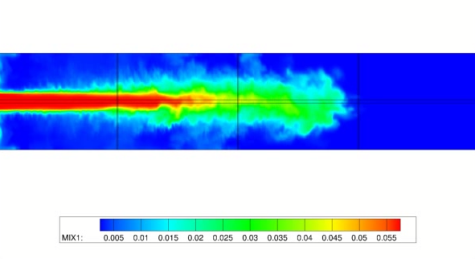
The optimization problem considered in this project contains a coupled systems of time-dependent PDEs, namely the flow governing Navier-Stokes equations and a set of scalar transport equations. The combination of the two PDE types can be used to describe combustion processes in a turbulent flow, as it occurs e.g. in combustion chambers of gas turbines used in power-plants.
As the system of PDEs resolving combustion processes in detail are very stiff and still hard to compute numerically, the detailed chemistry model is replaced in favor of the Flamelet Generated Manifolds method (FGM), using precalculated data, looked up by a small number of simulated scalar quantities, massively reducing the size of the PDE system, while still resolving the characteristics of the combustion.
From the mathematical point of view the resulting PDE system for the combustion is of a non-autonomous advection-diffusion type, with a nonlinear source term depending on the scalar quantities (semilinear).
The project aims to not only carry out theoretical results for the optimization with such a PDE system as contraint, but also aims to test optimization algorithms in the context of combustion numerically by augmenting simulation tools from the mechanical engineering departments using an adjoint approach for obtaining gradient information efficiently.
Contact: Cedric Sehrt, Stefan Ulbrich


