W. D. Bauer's calculations of his parametric overunity rotator -

simply refuted

By G. W. Bruhn, Darmstadt University of Technology

Abstract: After several updates in the past, W.D. Bauer released a new update of his note on the overunity properties of his parametric overunity rotator [1] recently. Though W. D. Bauer knows about the following very simple arguments against his new calculations by private communication, he insists upon being right, against all evidence. The following short note is an excerpt from a longer article [2], where the author showed that there are no OU effects at all in W.D. Bauer’s devices.

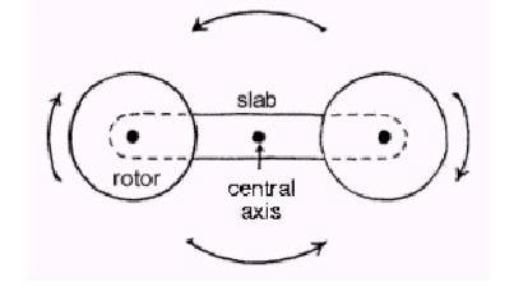
W.D. Bauer’s rotator consists of a rotating slab, the angular position of which in the plane is denoted by , and of a pair of rotors mounted symmetrically on the slab the angular position of which in the plane is denoted by . Separate driving motors on the central axis control the speed of both slab and rotors by means of belts. Let and denote the inertia moments of slab and the rotor pair, respectively. For further information the reader is referred to [1].

During a working cycle the rotator device travels through three phases: During phase 1 both the slab and the rotors are accelerated from rest to angular velocities and , respectively. During phase 2 the angular velocities are equalized by different methods. During phase 3 the whole device rotating with common angular velocity is brought back to rest by detracting its kinetic energy.

To show W. D. Bauer’s result to be erroneous we consider phase 2.

1. The driven rotors device

Let us first discuss the special case h = 1: At the beginning of phase2 the slab is decoupled from its drive motor such that it can rotate freely with its angular velocity due to its inertia. The rotors are rotating with the angular velocity , which has to be reduced by the rotor’s drive motor to the final smaller value at the end of phase 2. Evidently this can be done by detracting the difference of the rotational energies via the rotor’s drive motor, with other words, the negative amount of energy

has to be imported to the system, i.e. we obtain an energy gain. Instead of this, W.D. Bauer calculates the amount of energy (see (14) in [1])

by a complicated and dubious method. His result means, in contrast to all evidence, that a positive amount of energy has to be imported to the system via the rotors, in spite of the fact, that there is already a surplus of energy contained in the rotors.

The same consideration applies to all values of and all . Thus we conclude that W.D. Bauer’s formula (14) for the energy required for phase 2 (and hence his total energy balance (19)) is erroneous and cannot be true, while our result above is confirmed in [2].

2. A contradiction in W.D. Bauer’s treatment of the braked rotors device

W.D. Bauer discusses two other possibilities of equating the angular velocities of the rotors and the slab. The rotors are now braked against the slab:

A. By braking after having decoupled the slab from its driving motor.

B. By braking while the slab rotation is kept at constantly by its driving motor.

Case A: For the braking process of the rotors against the free slab W.D. Bauer obtains an energy loss during phase 2 of the size

(cf. (32) in [1]). We have checked this result and agree with it.

Case B: The braking is executed against the slab that is kept at constant by its driving motor. We can approximate case B by case A, if we assume the slab to have a very large momentum of inertia, i.e. if . Then the braking process will, due to the very large value of , not considerably influence the slab, i.e. the slab will approximately keep its angular velocity , with other words, the slab condition for case B is approximately fulfilled. Therefore we can expect to obtain the energy balance of phase 2 by neglecting in the denominator of the formula of above. This yields

.

as the energy balance of case B, which is an energy loss again as in case A. But W.D. Bauer’s result (43) in [1] is , which is negative, i.e. a gain of energy, for , a result, that is very amazing in view of the preceding case A. Therefore we cannot expect W.D. Bauer’s result (43) to be true, while our result above is confirmed in [2].

References

[1] W.D. Bauer: The parametric overunity rotator – the Wuerth power booster, (with last corrections on 3.10.00) at http://www.overunity.de/rotator/rotator2.htm

[2] G.W. Bruhn: W. D. Bauer's parametric overunity rotators - devoid of all overunity, available for the time being via W.D. Bauer’s References in [1]

The author: bruhn@mathematik.tu-darmstadt.de