K. Meyls Verletzung des 2.
Hauptsatzes in der Strömungsmechanik
Von G.W. Bruhn, Technische Universität Darmstadt
Von Zeit zu Zeit gibt es Versuche, eine Verletzung irgendeines Hauptsatzes nachzuweisen. Ein Versuch in der Strömungsmechanik stammt von K. Meyl, der seine Vorstellungen u.a. auf meteorologische Wirbel anwendet und an diesem Beispiel vorführt, wie es mit seinen Methoden zu einer Verletzung des 2. Hauptsatzes der Thermodynamik kommt. Dazu sei angemerkt, dass eine wesentliche Erkenntnis der Strömungsmechanik der letzten hundert Jahre besagt, dass die Entropie in Gasströmungen allenfalls zunehmen kann, wobei Entropiezunahme auf Reibung oder Verdichtungsstößen beruht.
1. Wirbelkonzentration nach K. Meyl
K. Meyl schreibt in [1], Bd.2 S.45-46:

K. Meyl präzisiert an keiner Stelle, was er unter einem "Wirbel" versteht. Indirekt ergibt sich aus seinem Text, dass es sich dabei um eine stationäre achsialsymmetrische Strömung eines reibungsfreien idealen Gases konstanter spezifischer Wärmen handeln soll. Auf jedem zur Wirbelachse (der z-Achse) koachsialen Kreiszylinder vom gegebenen Abstand r herrscht dann konstanter Gaszustand, der durch zwei Zustandsgrößen, z.B. Druck p=p(r) und Temperatur T=T(r) beschrieben werden kann. Alle weiteren Zustandsgrößen lassen sich auf Grund der in idealen Gasen gültigen Zustandsgleichungen aus p(r) und T(r) berechnen und sind damit gleichfalls nur von r abhängig. Dasselbe gilt auch von dem in Zylinderkoordinaten um die Wirbelachse beschriebenen Geschwindigkeitsvektor, der Radialgeschwindigkeit u= u(r) und der Tangentialgeschwindigkeit v= v(r). Die dritte Geschwindigkeitskomponente w= w(r) wird zu Null angenommen.
Meyl betrachtet nun in einer derartigen stationären achsialsymmetrischen Strömung eine "Wirbelkontraktion", das ist eine Verkleinerung des Radius r von r1 -> r2 , wie sie bei negativer Radialgeschwindigkeit u stattfinden würde (Tafel 12.8 in [1] Bd.2, s.u.), wobei Drehimpuls nach (12.22) (Massenerhaltung), sowie die Gesamtenergie nach Text auf S.45 konstant bleiben soll.

2. Überprüfung der Meylschen Rechnung
Wir wollen unter den genannten Annahmen die Rechnungen von Meyls Tafel 12.8 überprüfen:
Die Gleichung (12.24) zur Definition der kinetischen Energien enthält einen Schreibfehler, das mittlere Gleichheitszeichen ist ungültig, weil sonst nach (12.22) auch r1 = r2 gelten müsste.
Das Gleichheitszeichen in (12.25) zwischen dem Q-Quotienten und dem Quotienten der kinetischen Energien ist durch keine bekannte Gleichung der Strömungsmechanik gedeckt, der Rest der Gleichung hingegen richtig.
Der Fehler in (12.25) hat Konsequenzen: Während (12.27) ohne Beanstandungen bleibt, ist die aus (12.27) durch Einsetzen des Q-Quotienten gefolgerte Gleichung (12.28) für die Abkühlung falsch.
Die Formel (12.29) zeigt, dass K. Meyl offenbar einen isobaren Kontraktionsprozess des Wirbels annimmt. Dazu fehlt jede Begründung. Im Gegensatz dazu zeigen die Grundgleichungen der Gasdynamik, z.B. [5]:
Der
Kontraktionsprozess des Wirbels verläuft isentropisch.
3. Der Abkühlungseffekt bei Wirbelkontraktion
Dass in einem stationären Wirbel bei Kontraktion erhebliche Abkühlungen auftreten, ist seit langem bekannt und in der Literatur unter dem Stichwort "adiabatische Abkühlung" beschrieben (s. z.B. [3], S. 144, Sp. 2). Es handelt sich um eine einfache Konsequenz aus der in stationären Strömungen längs der einzelnen Stromlinien gültigen Bernoullischen Erhaltungsgleichung
![]()
(mit stromlinien-abhängiger Konstante): Wenn einer der Geschwindigkeitsterme u2 oder v2, z.B. v2 = c/ r2 stark anwächst, wie bei "Wirbelkontraktion", muss zur Kompensation der Temperaturterm entsprechend abnehmen. Die Bernoulli-Gleichung ist Ausdruck eines längs der einzelnen Stromlinien gültigen Energieerhaltungssatzes. Insofern hat K. Meyl mit seiner Eingangsbemerkung recht, dass der kontrahierende Wirbel die zur Kontraktion erforderliche kinetische Energie aus der Wärmeenergie (der Enthalpie) des Gases entnimmt. Nur schießt Meyl über das Ziel hinaus, indem er argumentiert, dass dies nur mit Entropieabnahme möglich sei. Aber auch die korrekte Behandlung mit konstanter Entropie liefert eine Temperaturabnahme. Für weitere Einzelheiten wird der Leser auf [4] und [5] verwiesen.
4. Korrekte Berechnung eines ebenen Wirbels
Für den Wirbel hat man nach [4] die folgenden drei Erhaltungssätze:
Die Bernoulli-Gleichung
![]()
und die tangentiale Impuls- und radiale Massenerhaltung
![]()
Dabei ist ![]() der Bezugszustand im
Abstand r0 von der Wirbelachse. Außerdem gilt für die vorliegenden
isentropischen Zustandsänderungen
der Bezugszustand im
Abstand r0 von der Wirbelachse. Außerdem gilt für die vorliegenden
isentropischen Zustandsänderungen
![]()
Setzt man ![]() , so geht (1) mit der
Abkürzung
, so geht (1) mit der
Abkürzung ![]() über in
über in
![]()
oder
![]()
d.h. mit (2-4) auch
![]()
was nach (r/r0 )2 aufgelöst werden kann:
![]()
Wegen (2), (3) sind dann auch (u/u0 )2 und (v/v0 )2 in Abhängigkeit von τ darstellbar:
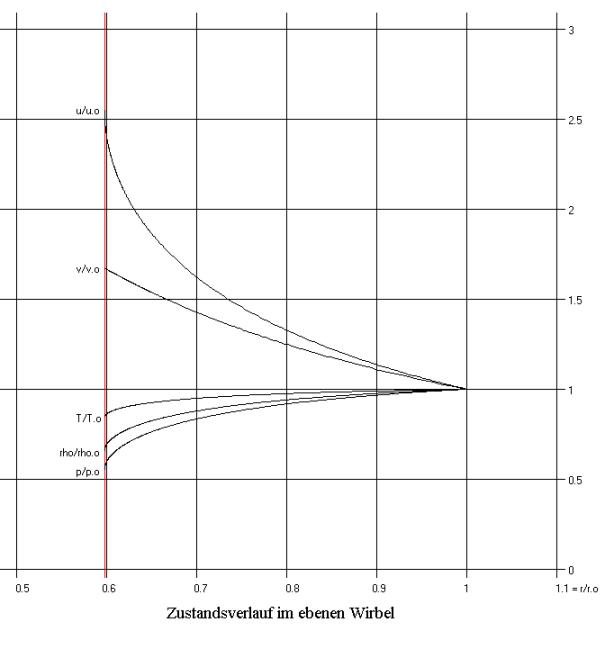
Die Auswertung dieser Parameterdarstellungen ab τ = 1 fallend liefert die folgenden Zustandsdiagramme im Beispielfall q2 = 30, sin2γ = cos2γ = 0.5.
Man sieht, dass die
Verläufe von u/u0 , p/p0 (und
auch T/T0) nach links mit vertikaler Tangente enden. Über diese
Grenze ist keine Fortsetzung der Strömung möglich. Der Massenabfluss über diese
Grenze muss bei technischer Realisierung durch Absaugen ausgeführt werden, wie
auch der Zufluss an der Stelle r = r0 technisch sichergestellt werden
muss.
Die Natur hilft sich am oder vor dem linken Rand, indem die Strömung in die 3. Dimension parallel zur Wirbelachse ausweicht, was mit dem ebenen Strömungsmodell natürlich nicht berechnet werden kann. Auch dreidimensionale Wirbel können (mit einigem Mehraufwand) berechnet werden.
Man beachte auch die erhebliche Temperaturabnahme im Wirbel von ca. 20% der absoluten Temperatur.
Literatur
[1] K. Meyl : Elektromagnetische Umweltverträglichkeit, Villingen-Schwenningen:
INTEL, Bd. 1,2, 3.Aufl. 1999, insbes. Bd. 2 S. 46 (ISBN 3-9802 542-9-1)
[2] Aufsätze von K. Meyl und andere Informationen
http://www.k-meyl.de/Meyl/meyl.html
http://www.k-meyl.de/Aufsatze/aufsatze.html
http://www.k-meyl.de/Meyl/meyl.html
http://www.k-meyl.de/Aufsatze/Buchbesprechung/buchbesprechung.html
[3] Hans J. Lugt, Vortex Flow in
Nature and Technology, WILEY 1973
[4] G. W. Bruhn, Zur Kontraktion des reibungsfreien Achsialwirbels,
http://www2.mathematik.tu-darmstadt.de/~bruhn/Wirbel_Kontrakt.htm
[5] G. W. Bruhn, Entropievernichtung und Selbstbeschleunigung in Navier-Stokes-Strömungen,
http://www2.mathematik.tu-darmstadt.de/~bruhn/Energie_diss.htm