Take
me back!
Spatial random permutations:
Some theory and a few pictures
Spatial random permutations:
Some theory and a few pictures
The basic model is very simple:
conside a planar square lattice, with
periodic boundary conditions. On the set of all permutations of the points
of the lattice, define a Gibbs measure with energy given by the sum of the
squared distances between every point and its image: i.e.

The following pictures are from a square lattice with side length 1000, and show the
points belonging to the 10 longest cycles of a typical random permutation obtained by
Markov chain Monte Carlo simulation. The three longest cycles are red, blue, green, in that
order. Clearly visible is the fractal nature of the random sets obtained, as well as the dependence
on the parameter beta.
Click on the small images for a larger image of the cycles!
Finally, below you can see a nice psychedelic work of art - this is what happens for really low beta,
i.e. around 0.1, on a really large grid of side length 2500.

periodic boundary conditions. On the set of all permutations of the points
of the lattice, define a Gibbs measure with energy given by the sum of the
squared distances between every point and its image: i.e.
The following pictures are from a square lattice with side length 1000, and show the
points belonging to the 10 longest cycles of a typical random permutation obtained by
Markov chain Monte Carlo simulation. The three longest cycles are red, blue, green, in that
order. Clearly visible is the fractal nature of the random sets obtained, as well as the dependence
on the parameter beta.
 |
 |
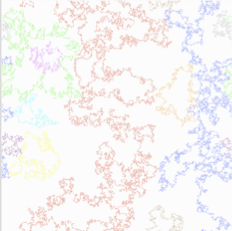 |
 |
| beta = 0.4 |
beta = 0.5 | beta = 0.6 |
beta = 0.7 |
Click on the small images for a larger image of the cycles!
Finally, below you can see a nice psychedelic work of art - this is what happens for really low beta,
i.e. around 0.1, on a really large grid of side length 2500.
